Exam for course Algorithms in Bioinformatics¶
Course number #22125/#22175.
June 25th 2023 10.00-12.00
The exam is open book meaning that you can seek information at the internet.
It is allowed to use generative AI (e.g., chatGPT) but please note:
- Make sure that you have read Study announcement s1885: Use of Artificial Intelligence (generative AI) in teaching and exams at DTU
- Importantly: "Always explicitly declare if any part of your submission is not your original work. Failure to do so may be considered exam cheating, in accordance with DTU's code of honour and the rules for referencing when using generative AI"
- More generally: generative AI is a tool that can (and should) be used to improve productivity much like other tools and sources of information. If you do use chatGPT to get information or write text, then you should (1) declare when you have done so, as specified above, (2) make sure the information is correct and relevant for the question being asked, (3) possibly rephrase, to get better and more correct responses.
- In my experience, chatGPT responses to previous exam questions have not been very good, often missing the point in my questions.
You however cannot consult other students taken the exam, and plagiarism is seriously condemned.
The total exam is 80 points.
Note, that you can compile your exam answers in any text editing program you prefer. You are NOT requested to use Jupyter-notebooks.
The exam must however be submitted via DTU Learn either as a jupyter-notebook or as a single PDF file via the course side at DTU Learn at the June 25th 2020 12.01 CEST. To create a PDF file, you might have to first save the file as HTML, open this file in your browser and safe/print it as PDF.
Please name you file as STUDENTID_NAME.pdf or STUDENTID_NAME.ipynb
import numpy as np
Question 1 (10 points)¶
Based on the single 3 letter sequence below
SEQ = AED
calculate the weight matrix using pseudo counts with a weight on prior $\beta = 5$, and next score the peptide
SEQ = FDK
against the matrix.
You can get the needed Blosum62 matrix from the link below.
BLOSUM62: https://teaching.healthtech.dtu.dk/morten_teaching/22125.algo/exam_2024/BLOSUM62
blosum62.freq_norm: https://teaching.healthtech.dtu.dk/morten_teaching/22125.algo/exam_2024/blosum62.freq_rownorm
Note, you might not need to use both of these matrices in the solution. Describe how you arrived at the result. Note, the solution is very simple if you think a little
Answer (the answer is the score of the peptide to the PSSM matrix including description of how to have arrived at the result)¶
Question 2 (25 points)¶
a)¶
Using the O2 algorithm, complete the accumulative alignment matrix D, the matrix P, the matrix Q and the E matrix below by replacing the missing values (AA, BB, CC, DD, and E) for the alignment of the two sequences
query = "LDEDEP"
database = "LDEDDEP"
using a scoring scheme with +5 for matches and -5 for all mismatches and gap penalties
gap_open = -5
gap_extension = -1
that is the score for match L to L is 5, and the score for matching E to D is -5. The database sequence, as always, is scored along the horizontal direction.
D Matrix
[ L D E D D E P
L [D1.XX 15.00 10.00 10.00 8.00 2.00 0.00 0.00]
D [15.00 20.00 10.00 15.00 10.00 3.00 0.00 0.00]
E [ 9.00 D2.XX 15.00 10.00 10.00 5.00 0.00 0.00]
D [ 7.00 10.00 9.00 10.00 15.00 5.00 0.00 0.00]
E [ 1.00 2.00 5.00 4.00 5.00 10.00 0.00 0.00]
P [ 0.00 0.00 0.00 0.00 0.00 0.00 5.00 0.00]
[ 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]]
P Matrix
[ L D E D D E P
L [P1.XX 5.00 5.00 3.00 -3.00 -2.00 -1.00 0.00]
D [15.00 9.00 10.00 5.00 -2.00 -2.00 -1.00 0.00]
E [P2.XX 10.00 5.00 5.00 0.00 -2.00 -1.00 0.00]
D [ 7.00 8.00 9.00 10.00 0.00 -2.00 -1.00 0.00]
E [ 1.00 2.00 3.00 4.00 5.00 -2.00 -1.00 0.00]
P [-5.00 -4.00 -3.00 -2.00 -1.00 0.00 -1.00 0.00]
[ 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]]
Q Matrix
[ L D E D D E P
L [Q1.XX 15.00 9.00 10.00 8.00 2.00 -4.00 0.00]
D [ 4.00 5.00 10.00 5.00 Q2.XX 3.00 -3.00 0.00]
E [ 2.00 5.00 4.00 5.00 10.00 4.00 -2.00 0.00]
D [-3.00 -3.00 0.00 -1.00 0.00 5.00 -1.00 0.00]
E [-2.00 -2.00 -2.00 -2.00 -2.00 -2.00 0.00 0.00]
P [-1.00 -1.00 -1.00 -1.00 -1.00 -1.00 -1.00 0.00]
[ 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00]]
E Matrix
[L D E D D E P
L [E1 2 1 2 E2 3 0 0]
D [4 1 2 1 1 3 0 0]
E [5 4 1 1 2 1 0 0]
D [5 1 5 1 1 2 0 0]
E [5 5 1 5 4 1 0 0]
P [0 0 0 0 0 0 1 0]
[0 0 0 0 0 0 0 0]]
In your answer, please include some details on how you have arrived at the obtained results.
Answer¶
D1.XX =
D2.XX =
P1.XX =
P2.XX =
Q1.XX =
Q2.XX =
E1 =
E2 =
Question 3 (5 points)¶
You are applying Metropolis Monte Carlo (Gibbs sampling) to minimize the error of a given predictor.
Your original configuration has an error of 0.7, and your updated configuration has an error of 0.8. What is the probability of accepting the updated configuration at a value of T=0.1?
In your answer, include some details on how you have arrived at the obtained result.
Answer¶
Question 4 (5 points)¶
You are applying SMM (or Ridge regression) to optimize parameters for a given predictor. You first do you the optimization with lambda equal to 1 (Model1), and next with lambda equal to 0 (Model2). After fitting the model, you calculate the sum of the magnitude (absolute value) of the parameters in the two models. What do you expect the outcome to be?
a) The sum is higher for the Model1 parameters
b) The sum is identical between Model1 and Model2
c) The sum is higher for the Model2 parameters
You must include some brief arguments for your answer
Answer¶
Question 5 (25 points)¶
The following figure describes an HMM model of an unfair casino playing “heads and tails” with a loaded coin (note, a picture should load below):
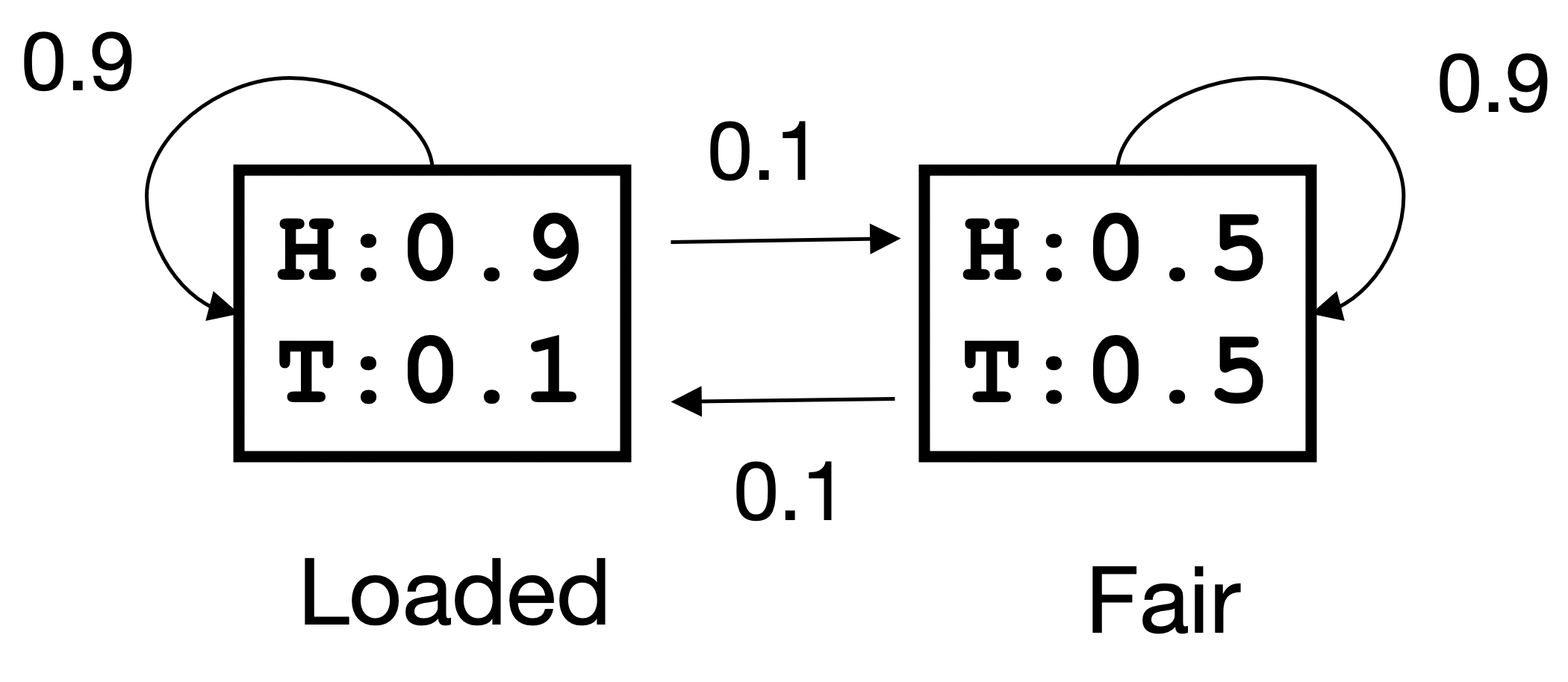
The arrows indicate the different transition probabilities and the values in the square the probabilities of getting head (H) and tail (T) with each of the two coins. When the model is used, a fair or loaded coin is selected at random initially.
a)¶
In the casino, you observed the following outcome TTHHHH after the casino has thrown the coin six times. Use the Forward algorithm to fill out the missing parts (X1 and X2) of the table below.
Forward Matrix:

In your answer, include details on how you have arrived at the obtained result.
Answer¶
X1 =
X2 =
c)¶
Given the backward matrix shown below (note, a picture should load below):
Backward Matrix:

and the Forward matrix from question a) what is the probability of the fourth observation ("H") being generated by the fair coin?
In your answer, include details on how you have arrived at the obtained result.
Answer¶
Question 6 (5 points)¶
The ANN below uses the step-function, with y=0, if x<=0, and y=1 otherwise, as activation function. Note, a picture should load below).
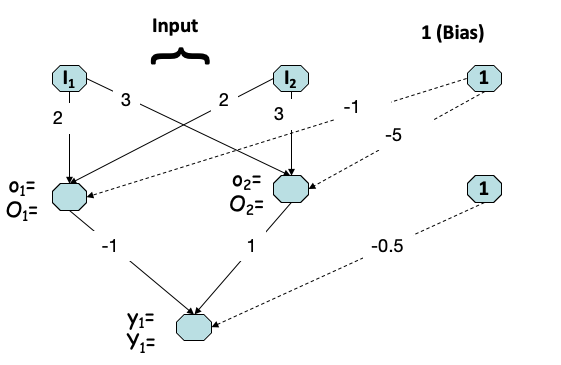
when the input values I1 and I2 are 0 or 1. Can this network describe the XOR function? In your answer, please include details on how you have arrived at the obtained result.
Answer¶
Question 7 (5 points)¶
When using Hobohm 1, which of the statements below are correct (you may select more than one)
a) Hobohm1 requires an all-against-all scoring?
b) When checking if an element is redundant it must be compared against all elements in the unique list?
c) When checking if an element is redundant it must only be compared against the first element in the unique list?
d) None of the above
Answer¶