Exam for course Algorithms in Bioinformatics¶
Course number #22125/#22175.
June 22th 2022 9.00-11.00
The exam is open book meaning that you can seek information at the internet. You however cannot consult other students taken the exam, and plagiarism is seriously condemned.
Note, that you can compile your exam answers in any text editing program you prefer. You are NOT requested to use Jupyter-notebooks.
The exam must however be submitted as a jupyter-notebook or a single PDF file via the course side at DTU Learn at the June 22th 2020 11.00 CEST. To create a PDF file, you might have to first save the file as HTML, open this file in your browser and safe it as PDF.
import numpy as np
Question 1 (15 points)¶
a)¶
From the sequences below:
IEK
IEK
TEK
TEA
TDK
IDA
calculate the weight matrix scores for I, and E at position 1 in the binding motif using pseudo counts with weight on prior $\beta = 5$ (ignoring sequence weighting). Describe how you arrived at the matrix scores by reporting the values of f (the observed frequency), g (the pseudo frequency), and p (the combined frequency), as well as the final weight matrix value, w, for each amino acid I and E.
Answer¶
c)¶
Calculate the weight matrix value for L at position 1 from an alignment containing 10000 peptide sequence where L is fully conserved at position 1. Assume that the weight on prior (or weight on pseudo count) is a fixed small number (<100) and ignore sequence weighting.
Include in some details on how you have arrived at the obtained result.
Answer¶
Question 2 (15 points)¶
a)¶
Using the O3 algorithm, complete the accumulative alignment matrix D and the E matrix below by replacing the X’s with the correct values for the alignment of the two sequences
query = "LDEDEP"
database = "LDEDDEP"
using the Blosum50 scoring matrix for matches and gap penalties
gap_open = -2
gap_extension = -1
and the database sequence, as always, is scored along the horizontal direction.
D_MATRIX = """
L D E D D E P
L XX 34 27 28 20 11 4 0
D 34 36 28 30 21 12 5 0
E 25 26 28 26 22 13 6 0
D 19 20 21 22 24 14 7 0
E 10 11 12 13 XX 16 8 0
P 3 4 5 6 7 8 10 0
0 0 0 0 0 0 0 0
"""
E_MATRIX = """
L D E D D E P
L X 2 1 2 3 3 3 0
D 4 1 1 1 1 3 3 0
E 5 4 1 1 2 1 3 0
D 5 1 5 1 1 2 3 0
E 5 5 1 5 X 1 2 0
P 5 5 5 5 5 4 1 0
0 0 0 0 0 0 0 0
"""
In your answer, please include some details on how you have arrived at the obtained results.
Answer¶
d_matrix[0,0] =
d_matrix[5,5] =
e_matrix[0,0] =
e_matrix[5,5] =
Question 3 (10 points)¶
You applying Metropolis Monte Carlo (Gibbs sampling) to minimize the error of a given predictor.
Your original configuration has a fitness of 0.5, and you updated configuration has a fitness of 0.7. What is the probability of accepting the updated configuration at a value of T=0.2?
In your answer, include some details on how you have arrived at the obtained result.
Answer¶
Question 4 (10 points)¶
You are applying SMM (or Ridge regression) to optimize parameters for a given predictor. You first do you the optimization with lambda equal to 0 (Model1), and next with lambda equal to 0.5 (Model2). After fitting the model, you calculate the sum of the magnitude (absolute value) of the parameters in the two models. What do you expect the outcome to be?
a) The sum is identical between Model1 and Model2
b) The sum is higher for the Model1 parameters
c) The sum is higher for the model2 parameters
Answer¶
Question 5 (25 points)¶
The following figure describes an HMM model of an unfair casino playing “head and tails” with a loaded coin (note, a picture should load below):
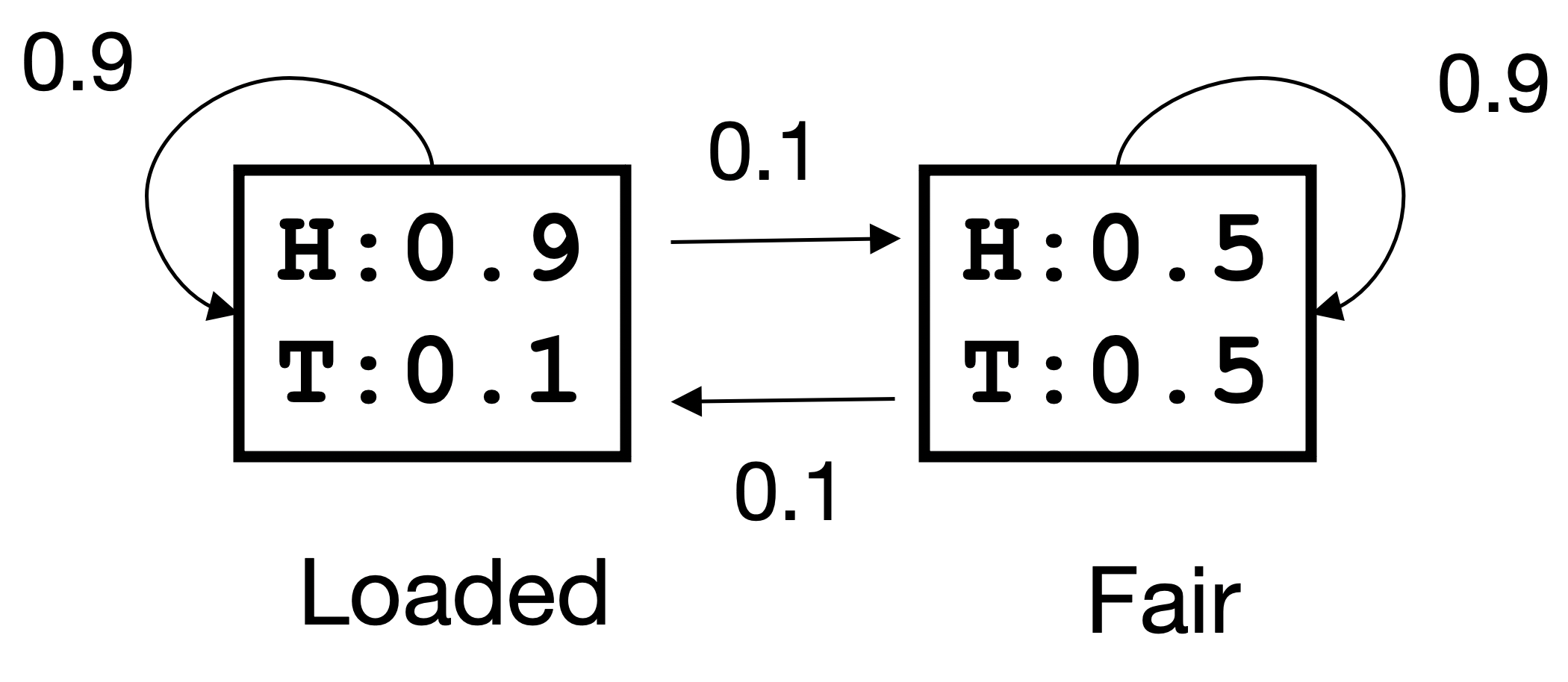
The arrows indicate the different transition probabilities and the values in the square the probabilities of getting head (H) and tail (T) with each of the two coins. When the model is used, a fair or loaded coin is selected at random initially.
a)¶
In the casino, you observed the following outcome HHTTHH after the casino has thrown the coin six times. Use the Viterbi algorithm to fill out the missing parts (XX) of the table below including the two missing arrows (note that we here use raw and NOT log-transformed probabilities).

In your answer, include details on how you have arrived at the obtained result.
Answer¶
Question 6 (10 points)¶
Calculate the output from the ANN below using the step-function as activation function with y=0, if x<=0, and y=1 otherwise. Note, a picture should load below).
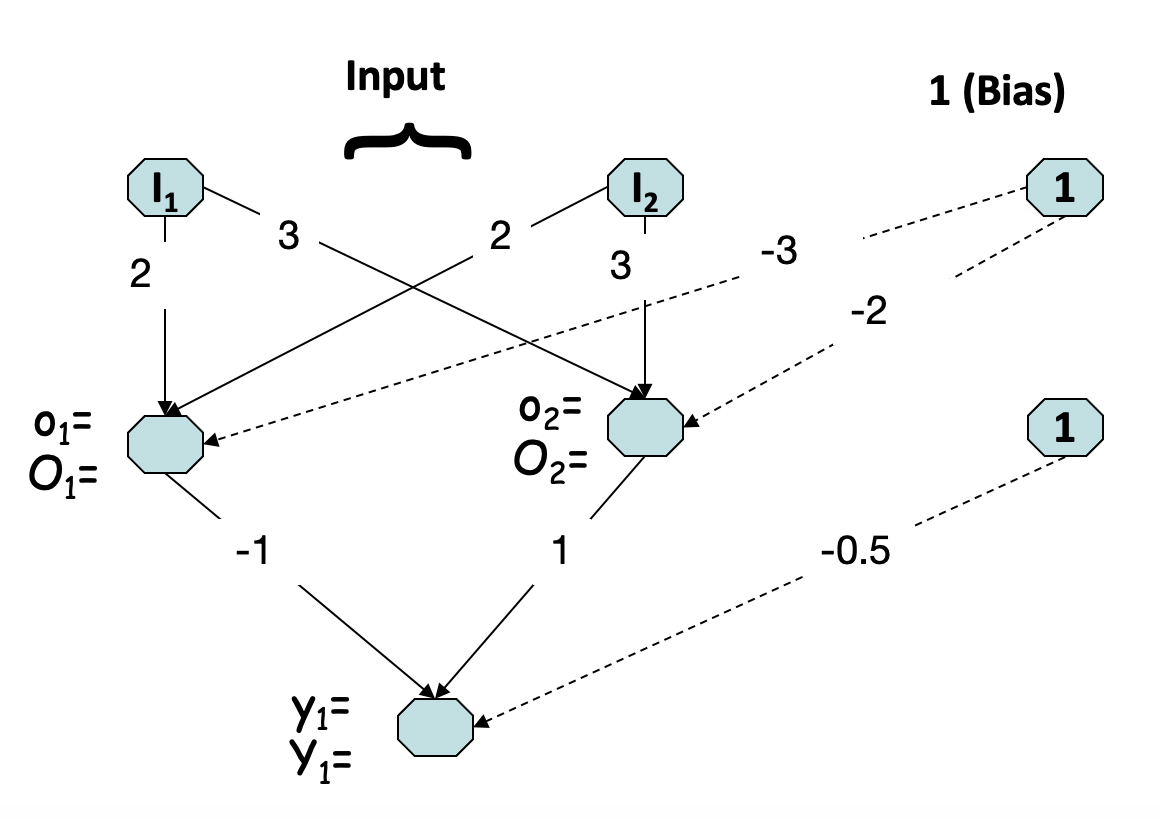
when the input values I1 and I2 are as given below. In your answer, please include some details on how you have arrived at the obtained result.
a)¶
I1 = 0
I2 = 1
Answer¶
Question 7 (15 points)¶
a)¶
From the alignment
ALLP
ALAK
ALAK
ALAK
ALAK
ALAK
GMNE
calculate the weight of the first peptide ALLP using heuristic sequence weighting. Note, that the peptide data set is NOT identical to the peptides from the lecture slides.
In your answer, please include details on how you have arrived at the obtained result.
Answer¶
You're done!¶