DiscoNet2 answers
Multiomics data integration exercise - Answers
Answers written by: Lars Rønn Olsen
First, load the data for today's exercise:
load("/home/projects/22140/exercise10.Rdata")
Then, randomly pick a patient number. Let's use R to make sure it is random:
mypt <- sample(1:10, 1)
For that patient calculate the log2 fold change of gene expression in cancer vs normal log2(cancer expression / normal expression). Consider genes with a log2 fold change either smaller than -1 (down regulated) or larger than 1 (up regulated) dysregulated. We also consider mutated genes (with a 1 in the mutation column) as aberrated (aka nonsynonymous), so you should keep these as well. Save a list of dysregulated and/or aberrated genes.
pt <- as.data.frame(data[[mypt]]) pt$log2fc <- log2(pt$tumor/pt$normal) pt$gene <- rownames(pt) seed <- rownames(pt[abs(pt$log2fc) > 1 | pt$mutation == 1,])

TASK/REPORT QUESTION #1:
- What patient did you pick?
- How many genes are up or down regulated?
table(abs(pt$log2fc) > 1)
Depends on your sample. Somewhere between 4 and 100.
- Is the number of dysregulated genes what you would expect from a disease like cancer?
Given that cancer arises from normal cells, you would expect the cancer cells to be somewhat similar to their cognate, normal cells. However, as we learned from reading the Hallmarks paper, cancer dysregulates a number of cellular functions, and for this I would probably guess between 100 and 1000 genes to be dysregulated.
- How many genes harbor nonsynonymous mutations (Note: we only report nonsynonymous mutations in this data. Synonymous mutations have already been removed)?
Depends on your sample. Somewhere between 1 and 32.
- Theoretical question: Discuss the biological connection, or lack thereof, between nonsynonymous mutations and de-regulated of a) mutation and expression of the same gene and b) mutations in one gene and the expression of other genes. Use a maximum of 75 words.
For the patient sample you picked, make a node attribute table containing the following columns: “Gene”, “log2FC”, “somatic_mutations” (either 0 or 1) for all genes.
Somatic mutations are stochastic events + selective pressure. Generally speaking, expression of a gene and its mutation status may not necessary correlate. However, in theory a loss of function mutation may activate a feedback loop increasing expression of the gene, and likewise a gain of function mutation may decrease expression resulting from feedback. Lastly, mutations of some genes may affect the expression of others. This is known as "expression quantitative trait loci"
Virtual pulldown
Load the DiscoNet package and prepare the inweb database:
library(DiscoNet) ### Load translated database load(file='/home/projects/22140/inweb_reduced.Rdata') # db
Then, use the virtual_pulldown() function that you used last week, to perform a virtual pulldown with all dysregulated and/or mutated genes.
network <- virtual_pulldown(seed_nodes = seed, database = db_reduced, id_type = "hgnc", zs_confidence_score = 0.156) interactions <- data.frame(network$network) node_attributes <- data.frame(network$node_attributes)

TASK/REPORT QUESTION #2:
- How does a virtual pulldown work?
It identifies proteins interacting with your input proteins, and…
- What experiment does it simulate?
…Simulates a complex pulldown experiment
- What database does it query?
The InWeb database of protein-protein interactions
- What does the confidence score mean?
The experimental confidence we have in the interaction
- Is the default cutoff of 0.156 reasonable? Why/why not?
In this context, it would appear so as we don’t get massive hairballs, nor do we get empty networks. In a real life research project, one would try multiple different thresholds and assess whether cluster member nodes share functional features to a degree where they can be considered a protein complex, or whether there a glaring outliers in terms of function, which should be filtered out
We changed the package based on your excellent feedback last week. Now, the virtual_pulldown() function produces an interaction table (in the $network object), with confidence scores as edge attributes and a node attribute table (in the $node_attributes object) with a seed indicator and a topological score for each node.
Use the merge() function to add log2FC and mutation status to the node attribute table. Here's a hint so you don't spend too much time on this:
node_attributes <- merge(x = node_attributes, y = pt, by.x = "nodes", by.y = "gene", all.x = TRUE)
Make sure you understand what goes on in the function above.
Use the function graph_from_data_frame() to make an igraph object. Remember to make it undirected and add node attributes.
g <- graph_from_data_frame(interactions, directed = FALSE, vertices = node_attributes)
Use the relevance_filtering() function to make 3 different versions of the pulldown, with cutoffs "0", "0.5", "0.8".
g1 <- relevance_filtering(g, 0.0) g2 <- relevance_filtering(g, 0.5) g3 <- relevance_filtering(g, 0.8)

TASK/REPORT QUESTION #3:
- How many nodes/edges are in your three pulldown networks? (answer depends on which patient you chose, but you can find out by examining the graph objects)
g1 g2 g3
- Plot the 0.8 filtered pulldown network, colored by log2FC and mutated genes highlighted with a shape, and seed nodes highlighted in some other way. Make sure the plots added to the report are easy to read.
ggraph(g3) + geom_edge_link() + geom_node_point(aes(color = log2fc, shape = as.factor(mutation)), size = 5) + scale_color_gradient2(low = "red", mid = "white", high = "blue")
- Does the networks look as you would expect in terms of which genes are up or down regulated or mutated? I.e. is the mutation status generally related to expression status? What would you expect?
For the following exercises use the network with a cutoff of 0.8
Community detection / protein complex inference
Run the community_detection() function with the MCODE algorithm with parameters D = 0.05, haircut = TRUE, fluff = FALSE. The resulting communities may represent protein complexes that could be causative or indicative of the disease.
communities <- community_detection(g3, algorithm = "mcode", D = 0.05, haircut = TRUE, fluff = FALSE, fdt = 0.8, loops = FALSE)

TASK/REPORT QUESTION #4:
- How many nodes/edges are in your top 25 scoring communities (note: you many not have this many, in which case just report nodes/edges for all of them)
lapply(communities[[1]], function(x) paste(vcount(x), ecount(x)))
- How is the community score from MCODE calculate and what does it mean?
- Have a quick look [here|https://en.wikipedia.org/wiki/Protein_complex]. What do you expect a protein complex to look like? How many proteins? What clustering coefficient (how densely clustered)? Why?
A protein complex is a group of proteins forming a quaternary structure to perform a given function. As such, one would not expect, e.g. five proteins linked together by single edges to form a long string to constitute a protein complex. Similarly, 200 proteins in a hairball probably wouldn’t be a protein complex either.
- Based on node/edge counts alone, which of your communities could be complexes?
Answer of course depends on your choice of patient sample, but generally you are looking networks with between 3 and 20ish nodes - pick a community that satisfies this and plot it
chosen_community <- 3
ggraph(communities$communities[[chosen_community]]) + geom_edge_link() + geom_node_point(aes(color = log2fc, shape = as.factor(mutation)), size = 5) + geom_node_text(aes(label = name), size = 10, repel = TRUE) + scale_color_gradient2(low = "red", mid = "white", high = "blue")
Gene ontology over-representation analysis
Now use the the fora() function from fgsea to perform an over-representation analysis on all the detected communities. Use the full list of genes from the exercise data as your background, and the biological process ontology.
library(fgsea) library(msigdbr) # First, fetch gene sets BP_df = msigdbr(species = "human", category = "C5", subcategory = "BP") BP_list = split(x = BP_df$gene_symbol, f = BP_df$gs_name) # repeat the analysis below with the communities you deem to be potential protein complexes fora(pathways = BP_list, genes = V(communities$communities[[1]])$name, universe = rownames(pt))
Note: If you get a timeout error just run the function again.

TASK/REPORT QUESTION #5:
- Why are we asking you to use the "full list of genes" from the microarray as the background, and not all human genes? (Note that microarrays, while comprehensive, do not have probes for every single human gene).
Because we don't know what the result would be for genes we did not measure
- What does an over-representation test do?
Whether certain GO terms are found at a higher frequency in a target list of genes than their frequency in background of all genes.
- What is “over-represented” and where?
GO terms in the target genes
Interpreting the results of the over-representation analysis
Relate functions of the significantly over-represented GO terms in each of the top 25 protein complexes to the hallmarks of cancer. Keep in mind that neither all complexes, nor all GO terms are necessarily related to cancer.

TASK/REPORT QUESTION #6:
- 6.1) Do any of your complexes relate to one or more of the hallmarks of cancer? How? (You will probably need to search Google here – try [GO term]+cancer or even [GO term]+”follicular thyroid cancer”).
This depends on your sample, your clusters, and how thorough you are at checking what your GO terms mean.
- 6.2) If you cannot reasonably relate some of the GO terms to a cancer hallmark (and it is not unlikely that you cannot!), why do you think these non-cancer related ontologies are over-represented?
Given that we are looking at thyroid tissue either way (healthy or sick), we expect some thyroid functions to turn up in the list.
- 6.3) Plot the three communities you find most interesting in the context of follicular thyroid cancer. Highlight log2FC, mutation status, and seed nodes
- 6.4) How do you think these dysregulated protein complexes may drive cancer pathogenesis?
- 6.5) For the targets of your three chosen protein complexes, pick the protein best suited as a drug target and explain why based on what you have learned about network topology.
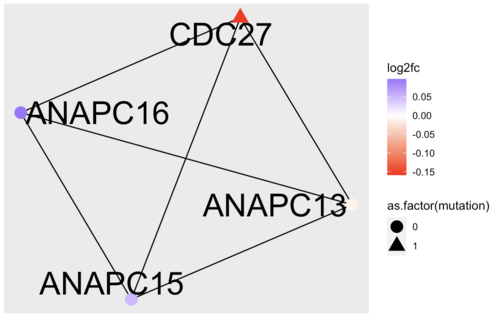
Again, the answers to the three questions above, depends on what sample you have been working on. I chose patient 1 and a relevance score cutoff of 0.8. My community number 2 looks like this:
Running an over-representation analysis of the complex, reveals multiple GO terms related to cell cycle and devision. Looking closer at the dysregulated genes in the complex, tells me that CDC27 might be the culprit here. I then decided to Google the gene and discovered that "CDC27 Facilitates Gastric Cancer Cell Proliferation, Invasion and Metastasis via Twist-Induced Epithelial-Mesenchymal Transition" (https://pubmed.ncbi.nlm.nih.gov/30308498/)
In terms of targeting, CDC27 seems like an obvious choice, since this is a small complex and all nodes have the same degree. Had the complex been larger, it could have made sense to look at the degree and betweenness centrality of the nodes as targeting hubs is a generally a good way disrupt a network