Model selection

This exercise is part of the course Computational Molecular Evolution (22115).

Overview

In this exercise you are going to investigate features of HIV-1 evolution. You will do this by analyzing a large set of env-genes from HIV-1, subtype B. specifically, the DNA sequences analyzed here correspond to a region surrounding the hypervariable V3 region of the gp120 protein.

Like other retroviruses, particles of HIV are made up of 2 copies of a single-stranded RNA genome packaged inside a protein core, or capsid. The core particle also contains viral proteins that are essential for the early steps of the virus life cycle, such as reverse transcription and integration. A lipid envelope, derived from the infected cell, surrounds the core particle. Embedded in this envelope are the surface glycoproteins of HIV: gp120 and gp41. The gp120 protein is crucial for binding of the virus particle to target cells, while gp41 is important for the subsequent fusion event. It is the specific affinity of gp120 for the CD4 protein that targets HIV to those cells of the immune system that express CD4 on their surface (e.g., T-helper lymphocytes, monocytes, and macrophages).

The role gp120 plays in infection and the fact that it is situated on the surface of the HIV particle, means it is an obvious target for the immune response. That means that there may be a considerable selective pressure on gp120 for creating immune-escape mutants, where amino acids in the gp120 epitopes have been substituted. In this exercise you will construct a maximum likelihood tree that we will subsequently use to investigate whether you can detect such a selective pressure on parts of gp120, again using maximum likelihood methods.

One major goal with the exercise is to introduce you to statistically based methods for assessing the strength of evidence for a set of alternative hypotheses about some biological system of interest. The model selection method we will use is AIC (Akaike Information Criterion), based on which you will compute model probabilities. A second goal is to make you aware that phylogenetic analysis is not only about constructing trees, but that it is also a useful framework for analyzing biological questions more generally.

Specifically, you will

1. perform a multiple alignment of gp120 DNA sequences taking protein-level information into account (using revtrans).
2. select a suitable nucleotide substitution model (using jmodeltest2)
3. construct a phylogenetic tree (using PAUP).
4. try to detect positively selected sites in gp120 (using PAML).

---

Recipe for computing AIC values and model probabilities

Later in today's exercise you will be asked to compute AIC values and model probabilities. Return to this section and follow the instructions when you need to do so.

1. Fit a set of models to your data, note the maximized log likelihoods (lnL) and the number of free parameters (K) for each model in the investigated set. The models you fit should represent a plausible and comprehensive set of hypotheses about your data.
2. Compute AIC for each of the models: AIC = -2 x lnL + 2K.
   For example: a model with lnL = -2010 and K = 5 will have AIC = -2 x -2010 + 2 x 5 = 4030.
3. Identify the model with the smallest AIC (this is the best model in the set). We will call the AIC for this model "AICmin".
4. Compute the "ΔAIC" values for each model: ΔAIC = AIC - AICmin
   For each model subtract the minimum AIC value. The best model will have a ΔAIC of zero. The rest of the models will have positive ΔAICs.
5. For each model compute the following quantity: numerator = exp(-0.5 x ΔAIC)
   For example, a model with ΔAIC=4.2 will have numerator = exp(-0.5 x 4.2) = exp(-2.1) = 0.1225. Also compute the sum of the numerator values for all models.
6. Finally, the model probabilities for each model are found as: P(model) = numerator / sum
   For example, if sum = 3.75 and a model has numerator = 1.3, then it has P(model) = 1.3 / 3.75 = 0.35

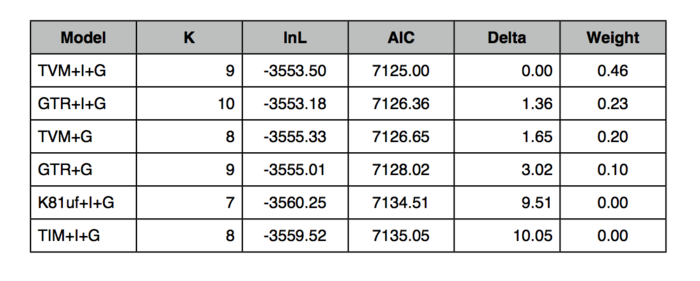
You may want to keep track of the computations by constructing a table along the following lines:

Note that model probabilities can also be computed using Bayesian methods. One advantage of Bayesian methods over AIC is that instead of relying on a point estimate, uncertainty about parameter values is accounted for by integrating over all possible values (typically using MCMC).

---

Getting started

Create working directory, copy files

In the command below: Instead of /path/to/molevol enter the path to the directory where you have placed your course files (for instance cd /Users/bob/Documents/molevol, or cd /home/student/molevol).

cd /path/to/molevol
mkdir modelselect
cd modelselect
cp ../data/gp120.fasta ./gp120.fasta
cp ../data/codeml.ctl ./codeml.ctl

Have a look at the DNA data file:

nedit gp120.fasta &

The file contains several DNA sequences from HIV-1, subtype B. The sequences are approximately 500 bp long, and correspond to a region surrounding the hypervariable V3 region in the gene encoding gp120. Close the nedit window when you've had a look.

---

Analysis of viral data set: alignment of coding DNA

DNA sequences are a lot less informative than protein sequences and for this reason it is always preferable to align coding DNA in translated form. The simple fact that proteins are built from 20 amino acids while DNA only contains four different bases, means that the 'signal-to-noise ratio' in protein sequence alignments is much better than in alignments of DNA. Besides this information-theoretical advantage, protein alignments also benefit from the information that is implicit in empirical substitution matrices such as BLOSUM-62. Taken together with the generally higher rate of synonymous substitutions over non-synonymous ones, this means that the phylogenetic signal disappears much more rapidly from DNA sequences than from the encoded proteins. It is therefore preferable to align coding DNA at the amino acid level.

However, in the context of molecular evolution, DNA alignments retain a lot of useful information regarding silent mutations. Especially the ratio between silent and non-silent substitutions is informative. We would therefore like to construct a multiple alignment at the DNA level, but using information at the protein level, and the RevTrans server does exactly that.

RevTrans takes as input an unaligned set of DNA sequences, automatically translates them to the equivalent amino acid sequences, constructs a multiple alignment of the protein sequences, and finally uses the protein alignment as a template for constructing a multiple DNA alignment that is in accordance with the protein alignment. This also means that gaps are always inserted in groups of three so reading frames are kept in order. That is important if you want to analyze selection, as we will in this exercise.

Construct RevTrans alignment

• Open RevTrans server page: https://services.healthtech.dtu.dk/services/RevTrans-2.0/
• On the RevTrans page: Choose the file gp120.fasta as input (or copy and paste the sequence into the sequence window)
• Click the "Submit query" button
• When the alignment is done you may have to click link named "here" to go to results page
• Download DNA alignment, by right-clicking the link for "Download alignment in FASTA format", and choosing "Save link as..." (save file under the name gp120align.fasta and make sure to save the file in the directory modelselect).

Convert alignment to NEXUS format

Convert the fasta file to NEXUS format and save file in the modelselect directory under the name gp120.nexus

---

Selection of substitution model using jmodeltest2

Question 1

As part of the present analysis we are going to build a phylogenetic tree based on the DNA alignment constructed above. We will construct the tree using maximum likelihood, but to do that we first have to decide which substitution model we want to use. Specifically, we are interested in using the model that best describes our data without having more parameters than strictly necessary (thus avoiding overfitting). We will investigate this issue by fitting a set of 56 different models to our data and then selecting one with a reasonable balance between model complexity and data fit.

Start jmodeltest2

jmodeltest

Load data set

• File -> Load DNA alignment -> File Format -> Select "All files"
• Navigate to gp120.nexus and load it

Fit 56 models

• Analysis -> Compute likelihood scores
• Select "7" under "Number of substitution schemes"
• Select "Fixed BIONJ-JC" under "Base tree for likelihood calculations"
• Click "Compute likelihoods"

This causes jmodeltest2 to perform the following actions: first a neighbor joining tree is constructed using the Jukes and Cantor model. Then the tree is fixed and used as the basis for fitting a set of 56 different models to the data. For each model, the estimated model parameters and the negative log-likelihood are recorded. In addition to varying sets of substitution rate parameters (JC, K2P, ...), some of these models also include extra parameters that take into account the presence of different rates between sites. This is done in two ways: (1) by fitting a gamma distribution of rates ("+G"), and (2) by allowing for a proportion of constant ("invariable") sites ("+I").

Wait until jmodeltest2 is done fitting all 56 models (this will take a little while depending on your computer).

Inspect result, manually check model probabilities for three models

• Results -> Show results table

For each model this table lists the negative log-likelihood ("-lnL"), the number of parameters ("p"), and estimates of all model parameters (excluding branch lengths).

Manually compute model probabilities for three substitution models

Use AIC-based model probabilities to investigate which of the following three substitution models are best at describing how the sequences have evolved:

• Jukes and Cantor with fraction of invariant sites (JC+I)
• Jukes and Cantor with gamma-distributed rates over sites (JC+G)
• Jukes and Cantor with invariant sites and gamma-distributed rates (JC+I+G)

Before you can do the computation you need to know the log likelihood and the number of parameters for each model. Locate these values in the table for the JC+I, JC+G, and JC+I+G models, and write them down. Close the window with the result table when you are done.

Make sure to get the signs right: the values reported in the table are -lnL values, so you will need to reverse the sign to get the lnL (the lnL values you write down should be negative).

Question: Use the recipe above to compute AIC values and model probabilities. Report the results in a table similar to the one shown above

---

Question 2 Based on the model probabilities: wich model has more support?

---

Question 3 Use modeltest program to select best model

What you just did manually for JC+I, JC+G and JC+I+G, jmodeltest2 can do automatically for the full set of 56 fitted models. Specifically, it uses the list of negative log likelihoods and parameter counts in the table to compute AIC and model probabilities, and uses this to select the model that best fits the sequence data:

• Analysis -> Do AIC calculations ->
• Select "Write PAUP* block"
• click "Do AIC calculations"
• Results -> Show results table
• Select "AIC" tab
• SHIFT+click on the header of the "weight" column. This sorts the rows according to model weight, in descending order.

Question: What model was selected by modeltest based on the AIC values?

---

Construction of phylogenetic tree using PAUP

Question 4

Close the results table. In the main window you should now scroll up to the lines giving PAUP commands that will implement the selected model. The command is enclosed between "BEGIN PAUP" and "END;" and should look something like this:

Lset Base=(0.4064, [...]

You will need to copy this command to a PAUP session in the next step.

Start PAUP

paup

Above you used jmodeltest2 to select the most suitable substitution model for the present data set. You will now use this model to construct a maximum likelihood tree. You will use PAUP for this purpose. (note: it is possible to create a maximum likelihood or a model-averaged tree directly from the jmodeltest2 program, but we will instead do it in PAUP in order to more clearly see each step that is taken).

Load alignment:

execute gp120.nexus

Set tree-building criterion to maximum likelihood

set criterion=likelihood

Set model parameters to winning estimates

Above you located a set of lines in the jmodeltest2 output giving a PAUP command that sets the model parameters to the estimates that were found using the winning model. Copy and paste this lset command (without the BEGIN and END parts) into the window where PAUP is running.

PASTE LSET COMMAND FROM MODELTEST RUN HERE

Find best tree using selected model

Still in the PAUP-window, enter the following command

hsearch swap=tbr start=nj

This command causes PAUP to perform a heuristic search for the best maximum likelihood tree. Once an initial tree has been constructed, the heuristic search proceeds by rearrangements of the "tree bisection and reconnection" type (TBR). We are using the model selected by modeltest, AND the parameter estimates found by modeltest on that model. You could also have chosen to simply estimate all the model parameters as part of this step (i.e., at the same time as finding the best tree), but fixing them improves speed tremendously. Findind the best tree should take a few minutes at most.

Save best tree to file

savetrees format=newick brlens=yes file=gp120tree.phy from=1 to=1

Quit program

quit

Have a look at the tree:

You have now produced an unrooted tree of the HIV sequences and saved it in the file gp120tree.phy. Note that in this exercise we will not be interested in the tree as such - our focus is instead on finding positive selection on a subset of codon positions and the tree is just something we need in order to be able to fit the different codon models to the data. If you want to see the tree, you can do so with the following command:

figtree gp120tree.phy &

There is no meaningful root placed in this tree, so you may want to choose the unrooted view (the third icon in the Layout section of the figtree window). Close the figtree window when you have had a look

Question: What is the negative log likelihood of the tree you just found?

---

Detection of positively selected sites in gp120

Question 5

There is much more to phylogenetic analyses than merely reconstructing trees. One interesting result of probabilistic methods, is that the parameters of a model will have their values determined as part of the optimization procedure. This means that once such a model has been fitted to the data, it is possible to investigate these estimated parameter values to learn features about the evolutionary history of the sequences under investigation. In the present example we will focus on investigating whether we can find positively selected sites in our data set, defined as sites where the dN/dS ratio is larger than 1. We do that by using a codon substitution model where the dN/dS ratio is one of its parameters.

A further strength of the probabilistic approach is that you get a probabilistic measure of how well any model fits the data. This means you can use a stringent approach to determine which model fits the data best. In this framework one uses likelihoods (probabilities of data given model) to determine which model fits the data best. As you saw above, it is for instance possible to compute AIC values and model probabilities from the likelihood values of fitted models, Since each model essentially corresponds to a hypothesis about the evolutionary history of the data, we can thus use a stringent statistical approach to decide which hypothesis best describes our data.

In outline, you will now use the following steps to investigate whether there is any evidence for positively selected codons in your data set:

• Fit model M1, which assumes there are two classes of codons in the sequence: some with dN/dS < 1, some with dN/dS=1.
• Fit model M2, which assumes 3 distinct classes of codons: two with dN/dS ratios as for M1, and one extra class with dN/dS > 1.
• Assess the strength of evidence for the two models using AIC-based model probabilities
• If M2 is better: identify the positively selected codons

Inspect the parameter file

nedit codeml.ctl &

The file "codeml.ctl" contains several settings that are relevant for running the program codeml. Find the following lines and ensure that the file contains these values:

seqfile =  gp120align.fasta:  name of alignment file
treefile =  gp120tree.phy: name of tree file
seqtype = 1: tells the program that our data consists of coding DNA.
NSsites = 1 2 : tells the program to analyze models M1 and M2.
cleandata = 1: tells the program to ignore positions with gaps.

The settings entered by us will cause codeml to analyze two hypotheses about dN/dS ratios. M1 says there are two classes of codons with different dN/dS ratios in the sequence: one class with dN/dS < 1 (codons under purifying or negative selection), and one class with dN/dS=1 (no selection - neutrally evolving sites). M2 says there are 3 distinct dN/dS ratios for different sites in the sequence: one class with dN/dS < 1, one class with dN/dS=1 (these are the same type of classes as for M1), and one class with dN/dS > 1 (corresponding to sites under positive selection). The value of the dN/dS ratios (for those classes that have dN/dS < 1 or dN/dS > 1), the fraction of sites belonging to each class, and the position of sites belonging to each class, are unknown at first and will be determined during the analysis.

Start the analysis

codeml

This will start the codeml program using the settings in the file codeml.ctl. Depending on your computer, this will take some minutes to finish. (You may be able to see how the optimization procedure results in progressively better fits: the likelihood increases, meaning that negative log-likelihood decreases, as the fit improves).

Inspect result file:

Wait for the run to finish, and then look at the result file:

nedit selection.results &

This file contains a wealth of information concerning your analysis. The top part of the file gives an overview of your sequences, codon usage and nucleotide frequencies. You can ignore this information for now, and move on to the interesting part, namely the model likelihoods and parameter values:

Find likelihood, and number of free parameters for model M1

Search ==> Find... ==> enter "Model 1" and click Find

You are now in the region of the result file where the model likelihoods and parameter estimates are noted. Now, locate a line that looks a bit like the one shown below:

lnL(ntime: 72  np: 74):  -4242.470345     +0.000000

Identify the number of "free parameters", K, used in model M1: This is indicated by "np", and is 74 in the example shown above (most of these parameters are branch lengths in the tree; specifically, the number of branch length parameters is indicated by "ntime", and is 72 in this example). Also note the log-likelihood of the fitted model. This is the number right after the parenthesis, and is -4242.470345 in the example here.

Question: What are the values of K and lnL for model M1?

---

Question 6

Find dn/dS ratios and codon class proportions for model M1:

Scroll down a few lines until you get to a small table similar to this:

      dN/dS for site classes (K=2)
      p:   0.75111  0.24889
      w:   0.06583  1.00000

This gives a summary of the dN/dS ratios that were found in the data set. The line starting w: lists the two dN/dS ratios that were found (in this case 0.06583 and 1.00000 - the last one was pre-specified by us as part of the model and was therefore not a free parameter). The line starting p: gives the proportion of codon sites belonging to each of the dN/dS ratio classes (in the example above approximately 75% belong to the first class , while 25% of all sites belong to the class having dN/dS=1.00000).

Question: What are the dN/dS value (w) and proportion (p) of sites for both classes. Report the following values: p(class1), w(class1), p(class2), w(class2)

---

Question 7

Find likelihood, and K for model M2

Scroll past the M1 output until you get to the results for model M2.

Question: What are the values of K and lnL for model M2?

---

Question 8

Find dn/dS ratios and codon class proportions for model M2:

Now, scroll down a few lines until you get to a small table similar to the one you examined for M1 before. For this model there are 3 separate classes of codons.

Question: What are the dN/dS value (w) and proportion (p) of sites for all three classes? Report these values: p(class1), w(class1), p(class2), w(class2), p(class3), w(class3)

---

Question 9

Assess strength of evidence for models M1 and M2:

M2 will always have a better (higher) log-likelihood than model M1 because M2 has more free parameters, and M1 is nested within M2. You should now use the recipe given above to compute AIC values and model probabilities for M1 and M2.

Question: Report: AIC, ΔAIC, w (model probability) for M1 and M2

---

Question 10: Is M2 better than M1?

---

Question 11

Examine list of positively selected sites

If your M2 is clearly better than M1 (I firmly believe it should be if you did things according to instructions...), then you have evidence for the existence of positively selected sites in the gp120 gene. Now, scroll down to the end of the result file and locate a list similar to the one below. Note: This is the "Bayes Empirical Bayes" table, not the "Naive Empirical Bayes" table.

Bayes Empirical Bayes (BEB) analysis
Positively selected sites

         Prob(w>1)     mean w

    25 A 0.959*        3.133 +- 0.769
    27 P 0.906         2.990 +- 0.877
    56 K 0.987*        3.197 +- 0.687
    59 V 0.915         3.032 +- 0.873
    78 R 0.637         2.351 +- 1.129
    88 K 0.573         2.148 +- 1.077
    95 V 0.925         3.046 +- 0.843
    ...

It is not important what the distinction is in this context, but very briefly NEB ignores the fact that there is uncertainty about maximum likelihood estimates, especially for smaller data sets (for instance w for some codon is perhaps not exactly 3.046, but could be in a region around that value), while BEB accounts for that uncertainty.

This gives you a list of which residues (if any) that were found to belong to the positively selected dN/dS-class. Also listed is the probability that the site really is in the codon class where dN/dS > 1, and a weighted average of the w at the site. Using only DNA sequences you have now identified likely epitopes on the gp120 protein.

Question: List all sites having more than 95% probability of belonging to the positively selected class